2025内蒙古行测数量关系,均值不等式求极值
 内蒙古公务员考试行测数量关系考点累积
内蒙古公务员考试行测数量关系考点累积 、
、 内蒙古公务员考试行测数量关系技巧
内蒙古公务员考试行测数量关系技巧
极值问题是行测数量关系中较为常见的一类问题,其中均值不等式求极值,大家在学生时代接触过,但现在可能感觉既陌生又熟悉,印象已经并不深刻了。今天,小编整理了有关均值不等式求极值的知识点,为大家答疑解惑。
 例题讲解,做好笔记
例题讲解,做好笔记
一、概念
若a,b是实数,则 ,等号当且仅当a=b的时候取得。
,等号当且仅当a=b的时候取得。
二、推论
和定差小积最大,当正实数a、b的和为定值时,当且仅当a=b,a与b的乘积可取到最大值。
三、应用
【例1】某商品的进货单价为80元,销售单价为100元,每天可售出120件。已知销售单价每降低1元,每天可多售出20件。若要实现该商品的销售利润最大化,则销售单价应降低的金额是:
A.5元
B.6元
C.7元
D.8元
答案:C
【解析】设应降低x元,总利润为y元,则降低后的销售单价为(100-x)元,销量为(120+20x)件,进货单价为80元,则总利润y=(100-x-80)×(120+20x),将其化简成函数式为 ,根据一元二次函数图像性质,当
,根据一元二次函数图像性质,当 时,y最大。故本题选C。
时,y最大。故本题选C。
【例2】某类商品按质量分为8个档次,最低档次商品每件可获利8元,每提高一个档次,则每件商品的利润增加2元。最低档次商品每天可产出60件,每提高一个档次,则日减少5件。若只生产其中某一档次的商品,则每天能获得的最大利润是()元。
A.620
B.630
C.640
D.650
答案:C
【解析】设提高x档,则每件产品的利润增加2x元,日产量减少5x件,总利润为y元,每天获得的利润为y=(8+2x)×(60-5x)=10×(4+x)×(12-x)元,因为(4+x)+(12-x)=16是定值,根据均值不等式原理,故当且仅当4+x=12-x时,即x=4时,(4+x)×(12-x)的值最大,即可获得最大利润,为10×(4+4)×(12-4)=640元。故本题选C。
 例题讲解,做好笔记
例题讲解,做好笔记
但不管是哪种情况,函数总是对称的,所以必然会在对称轴位置处取得极值。那么对称轴怎么求呢?我们可以令函数等于0,得到函数图像与x轴的两个交点,利用函数图像的对称性,找到两个交点的正中间值,即为对称轴的位置。下面让我们来一起做两道题加深一下理解:
例1、厂家生产销售某新型节能产品,产品生产成本是168元,销售定价为238元,一位买家向该厂家预定了120件产品,并提出如果产品售价每降低2元,就多订购8件。则该厂家在这笔交易中所能获得的最大利润是( )元。
A.17920
B.13920
C.10000
D.8400
【解析】C。由题目所给信息,我们知道所求为总利润的最大值。又因为总利润=单件利润×销售量,所以需要把单件的利润以及销售量分别表示出来。具体来看,每一件产品的利润为238-168=70(元),售价每降低2元,利润也会跟着降低2元,所以在这不妨假设售价降低了x个2元,对应单件的利润应表示为(70-2x)元;原销售量为120件,并且售价每降低2元,销售量就会增加8件,因此销售量应表示为(120+8x)件。故总利润为(70-2x)×(120+8x)元。所求为最大利润,即这个函数的极大值。
在这里我们可以利用一元二次函数图像的对称性来求解,先让函数的值等于0,即令:(70-2x)×(120+8x)=0,解得:x1=35或x2=-15。由其对称性可知,x1和x2必关于对称轴对称,换言之,函数图像的对称轴正好位于x1和x2的正中间,即函数的对称轴为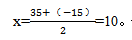 也就是说当x=10时,能获得最大利润。代入原函数,最大利润为(70-2×10)×(120+8×10)=10000(元),故选C。
也就是说当x=10时,能获得最大利润。代入原函数,最大利润为(70-2×10)×(120+8×10)=10000(元),故选C。
例2、某木苗公司准备出售一批木苗,如果每株以4元出售,可卖20万株,若木苗单价每提高0.4元,就会少卖10000株。那么,在最佳定价的情况下,该公司的最大收入是多少万元?
A.30
B.60
C.90
D.100
【解析】C。题目所求为最大收入,而收入=单价×销售量,因此我们需要把单价和销售量分别表示出来。先来看单价,单价为4元,设提高了x个0.4元,则单价=(4+0.4x)元;销售量为20万株,单价每提高0.4元,销售量便减少1万株,所以销售量=(20-x)万株。
因此收入=(4+0.4x)×(20-x)万元,所求的收入最大值就是求这个一元二次函数的极大值。可以利用函数的对称性来求解。令:(4+0.4x)×(20-x)=0,解得x1=-10或x2=20,由其对称性可知,x1和x2必关于对称轴对称,则函数的对称轴为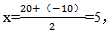 ,即当x=5时,收入最大,最大收入为(4+0.4×5)×(20-5)=90(万元),故选C。
,即当x=5时,收入最大,最大收入为(4+0.4×5)×(20-5)=90(万元),故选C。
以上就是关于一元二次函数求极值的题目,希望大家能够借助上述题目把这个知识点搞懂、吃透。
 更多数量关系技巧与方法扫码获取
更多数量关系技巧与方法扫码获取


扫码关注我们
极值问题是行测数量关系中较为常见的一类问题,其中均值不等式求极值,大家在学生时代接触过,但现在可能感觉既陌生又熟悉,印象已经并不深刻了。今天,小编整理了有关均值不等式求极值的知识点,为大家答疑解惑。
 例题讲解,做好笔记
例题讲解,做好笔记 一、概念
若a,b是实数,则 ,等号当且仅当a=b的时候取得。
,等号当且仅当a=b的时候取得。
二、推论
和定差小积最大,当正实数a、b的和为定值时,当且仅当a=b,a与b的乘积可取到最大值。
三、应用
【例1】某商品的进货单价为80元,销售单价为100元,每天可售出120件。已知销售单价每降低1元,每天可多售出20件。若要实现该商品的销售利润最大化,则销售单价应降低的金额是:
A.5元
B.6元
C.7元
D.8元
答案:C
【解析】设应降低x元,总利润为y元,则降低后的销售单价为(100-x)元,销量为(120+20x)件,进货单价为80元,则总利润y=(100-x-80)×(120+20x),将其化简成函数式为 ,根据一元二次函数图像性质,当
,根据一元二次函数图像性质,当 时,y最大。故本题选C。
时,y最大。故本题选C。
【例2】某类商品按质量分为8个档次,最低档次商品每件可获利8元,每提高一个档次,则每件商品的利润增加2元。最低档次商品每天可产出60件,每提高一个档次,则日减少5件。若只生产其中某一档次的商品,则每天能获得的最大利润是()元。
A.620
B.630
C.640
D.650
答案:C
【解析】设提高x档,则每件产品的利润增加2x元,日产量减少5x件,总利润为y元,每天获得的利润为y=(8+2x)×(60-5x)=10×(4+x)×(12-x)元,因为(4+x)+(12-x)=16是定值,根据均值不等式原理,故当且仅当4+x=12-x时,即x=4时,(4+x)×(12-x)的值最大,即可获得最大利润,为10×(4+4)×(12-4)=640元。故本题选C。
 例题讲解,做好笔记
例题讲解,做好笔记 但不管是哪种情况,函数总是对称的,所以必然会在对称轴位置处取得极值。那么对称轴怎么求呢?我们可以令函数等于0,得到函数图像与x轴的两个交点,利用函数图像的对称性,找到两个交点的正中间值,即为对称轴的位置。下面让我们来一起做两道题加深一下理解:
例1、厂家生产销售某新型节能产品,产品生产成本是168元,销售定价为238元,一位买家向该厂家预定了120件产品,并提出如果产品售价每降低2元,就多订购8件。则该厂家在这笔交易中所能获得的最大利润是( )元。
A.17920
B.13920
C.10000
D.8400
【解析】C。由题目所给信息,我们知道所求为总利润的最大值。又因为总利润=单件利润×销售量,所以需要把单件的利润以及销售量分别表示出来。具体来看,每一件产品的利润为238-168=70(元),售价每降低2元,利润也会跟着降低2元,所以在这不妨假设售价降低了x个2元,对应单件的利润应表示为(70-2x)元;原销售量为120件,并且售价每降低2元,销售量就会增加8件,因此销售量应表示为(120+8x)件。故总利润为(70-2x)×(120+8x)元。所求为最大利润,即这个函数的极大值。
在这里我们可以利用一元二次函数图像的对称性来求解,先让函数的值等于0,即令:(70-2x)×(120+8x)=0,解得:x1=35或x2=-15。由其对称性可知,x1和x2必关于对称轴对称,换言之,函数图像的对称轴正好位于x1和x2的正中间,即函数的对称轴为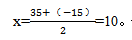 也就是说当x=10时,能获得最大利润。代入原函数,最大利润为(70-2×10)×(120+8×10)=10000(元),故选C。
也就是说当x=10时,能获得最大利润。代入原函数,最大利润为(70-2×10)×(120+8×10)=10000(元),故选C。
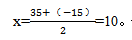 也就是说当x=10时,能获得最大利润。代入原函数,最大利润为(70-2×10)×(120+8×10)=10000(元),故选C。
也就是说当x=10时,能获得最大利润。代入原函数,最大利润为(70-2×10)×(120+8×10)=10000(元),故选C。 例2、某木苗公司准备出售一批木苗,如果每株以4元出售,可卖20万株,若木苗单价每提高0.4元,就会少卖10000株。那么,在最佳定价的情况下,该公司的最大收入是多少万元?
A.30
B.60
C.90
D.100
【解析】C。题目所求为最大收入,而收入=单价×销售量,因此我们需要把单价和销售量分别表示出来。先来看单价,单价为4元,设提高了x个0.4元,则单价=(4+0.4x)元;销售量为20万株,单价每提高0.4元,销售量便减少1万株,所以销售量=(20-x)万株。
因此收入=(4+0.4x)×(20-x)万元,所求的收入最大值就是求这个一元二次函数的极大值。可以利用函数的对称性来求解。令:(4+0.4x)×(20-x)=0,解得x1=-10或x2=20,由其对称性可知,x1和x2必关于对称轴对称,则函数的对称轴为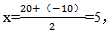 ,即当x=5时,收入最大,最大收入为(4+0.4×5)×(20-5)=90(万元),故选C。
,即当x=5时,收入最大,最大收入为(4+0.4×5)×(20-5)=90(万元),故选C。
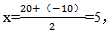 ,即当x=5时,收入最大,最大收入为(4+0.4×5)×(20-5)=90(万元),故选C。
,即当x=5时,收入最大,最大收入为(4+0.4×5)×(20-5)=90(万元),故选C。 以上就是关于一元二次函数求极值的题目,希望大家能够借助上述题目把这个知识点搞懂、吃透。
 更多数量关系技巧与方法扫码获取
更多数量关系技巧与方法扫码获取

点击分享信息:
 相关文章
相关文章


